A Bitcoin közgazdaságtana: útmutató a kínálati oldal megértéséhez

Azt már tudjuk, hogy a Bitcoin szűkös, és a bányászat nem fog örökké tartani. De mégis hogy jön ki, hogy mennyi az annyi? Vessünk egy pillantást a BTC kínálati képletére, és nézzük meg, hogy miről is szól a közgazdaságtana.
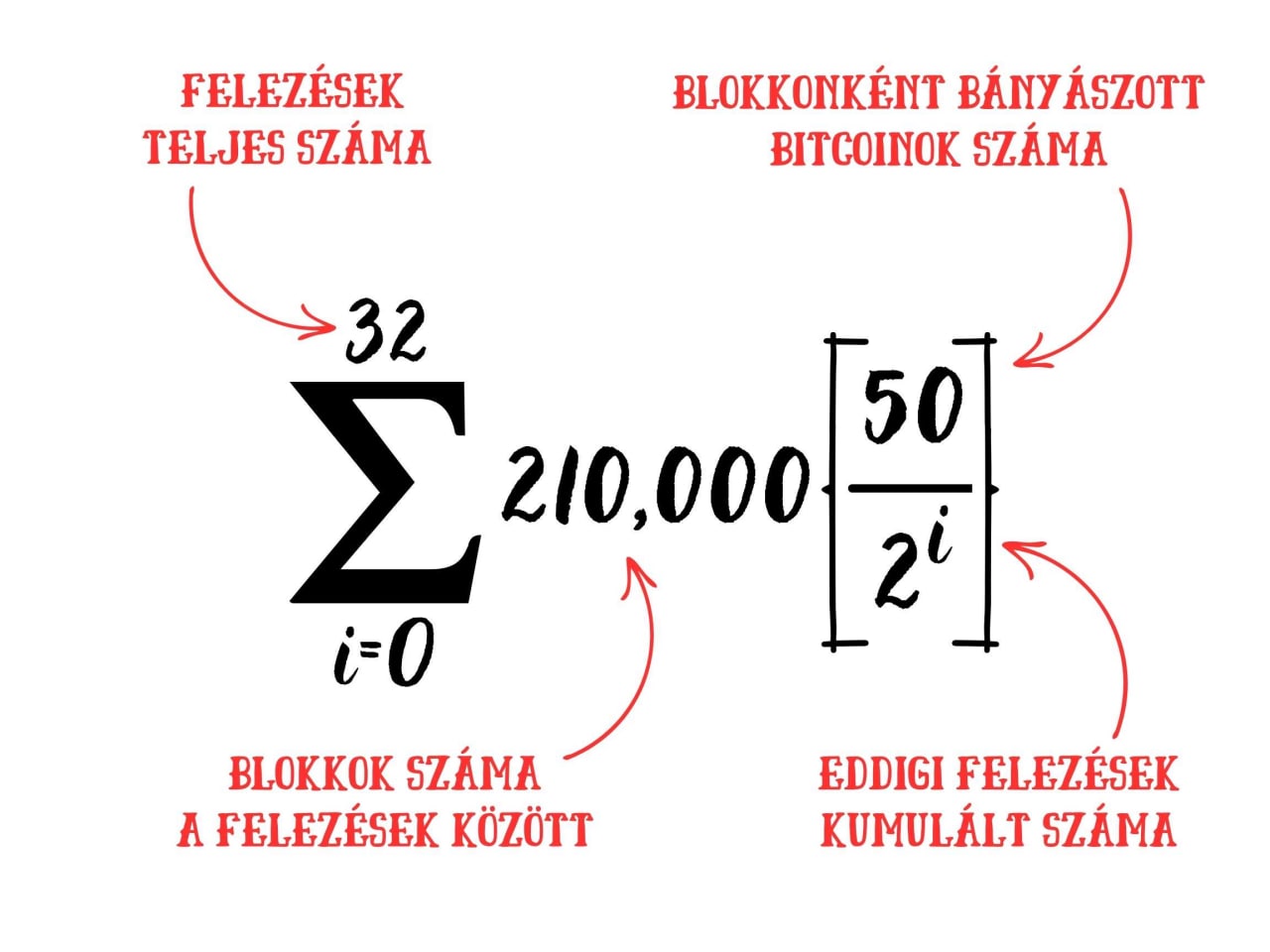
A Bitcoin protokoll gépezete rendkívül összetett: az elliptikus görbe matematikájától kezdve, a bonyolult algoritmusokon és kriptográfián át, egészen a legagyafúrtabb katonai stratégákat is lenyűgöző játékelméleti rétegekig. A Bitcoin-protokoll néhány kulcsfontosságú jellemzője, például a kínálati plafon, a felezés, a blokkjutalmak és a kínálat kiadása egy nagyon egyszerű matematikai képlettel (1. ábra) írható le, amely nem más, mint a Bitcoin kínálati képlet:
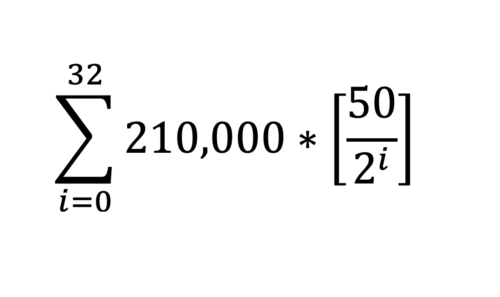
1. ábra: A Bitcoin kínálata leírható ezzel az elsőre ijesztőnek tűnő képlettel
Még mielőtt belevágnánk, fontos, hogy megértsük, mi is az az epocha. Az epochát egész egyszerűen tetszőleges időszakként értelmezhetjük. Az epocháknak nem feltétlenül kell pontosan meghatározottnak lenniük. Például egy hosszú, két átszállásos repülőút három epochaként határozható meg. Az első átszállás után azt mondhatjuk, hogy most vagyunk az utazás „második epochájában”.
Ha nem voltál erős matekból, vagy már régóta nem foglalkoztál matematikai problémákkal, első pillantásra ez a BTC képlet zavaros, sőt egyenesen ijesztő lehet. De ha lebontjuk az egyes részeket, pontosan megérthetjük, mi is történik ebben a híres képletben.
Ahogy fentebb utaltunk rá, a képlet egyes elemei a Bitcoin protokoll működéséhez kapcsolódnak. Nézzük meg, hogy mik ezek a fogalmak és számok, és mit is jelentenek tulajdonképpen (2. ábra).
Egyszerű levezetés a Bitcoin kínálati képlethez
A Bitcoin kínálati képlet gyakorlatilag egy matematikai összegző függvény. De mi a csuda az az összegző függvény? Egész egyszerűen egy sor összeadásról van szó.
Most pedig megnézzük a megértés szempontjából fontos matematikai kifejezéseket, majd az illusztráció érdekében egy egyszerű példával folytatjuk:
∑ (szigma) – A szigma szimbólum (∑) a matematikai szimbólum az összegzésre. Ehhez a szimbólumhoz jönnek hozzá általában az úgynevezett határok.
A határok – mint fent említettük, ezek a határok az összegző függvényünkhöz kapcsolódnak. Ezek a matematikai utasítások azokat a határokat jelölik, amelyeken belül a matematikai problémánk megoldása során dolgozhatunk. Ebben az esetben ezek a határok i=0-tól i=32-ig terjednek, az i=32-t is beleértve.
Az összegző függvények és határok fogalmainak megértéséhez nézzünk meg egy sor egyszerű egyenletet:

Példa az összegző függvényre
Az összegző függvény tehát pont olyan egyszerű, mint ahogy fent felvázoltunk: gyakorlatilag egy sor egyenlet eredményeinek összeadása. De hogyan lehetne ezt jobban reprezentálni és kifejezni úgy, hogy ne kelljen begépelnünk 3 külön egyenletet?
Itt jön a képbe az algebra.
Tudom, tudom, sokunkat már az algebra szó hallatán is lever a víz. Szinte görcsbe rándul a gyomrunk, amikor eszünkbe jut, hogy megizzadtunk vele a vizsgaidőszakban. Valójában azonban nem annyira ijesztő, egyszerűen arról van szó, hogy betűket használunk a számok meghatározására, amelyet általában változónak nevezünk. Egy változó csupán egy olyan szám, amelynek az értékét nem ismerjük, vagy egy szám, amely „változhat”.
A fenti egyenletek példáiban cseréljük le az egyenletek második számát az „x” betűre, és az így kapott egyenletet nevezzük A) egyenletnek.

A) egyenlet
Ezekben az esetekben az x volt a változó, amelynek értéke minden egyenletben változott.
Hogyan tudjuk még tömörebben kifejezni azt, amit fent akartunk elérni? A korábban említett határok felhasználásával megtehetjük. Nézzünk meg egy új egyenletet, és derítsük ki, mit is jelent ez pontosan:
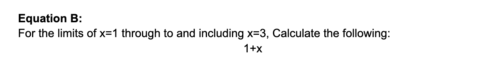
B) egyenlet
Egyszerűen menjünk végig az egyenleten, és tegyük pontosan azt, mint amit fent az A egyenletben tettünk: végezzük el minden lehetséges x értékre, amelynek határait 1-től 3-ig határozták meg. Mindezt még egyszerűbben is közölhetjük matematikai jelölések használatával, ami a következőképpen néz ki:
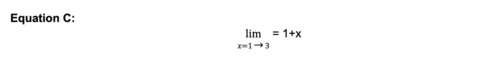
C) egyenlet
A C) egyenlet lényegében azt mondja: „Van 3 egyenletem, amit szeretnék megoldani. Az első egyenlet, amikor x=1, a másodiknál x=2, és végül a harmadik eset az x=3. És azt szeretném, hogy végezzükk el az 1+x műveletet.” Ez csupán annyit jelent, hogy 3 különálló egyenletet szeretnénk megoldani.
A végén viszont az egészet össze akarjuk adni. És hogyan írhatjuk le matematikai jelölések használatával, hogy össze is akarjuk adni őket? Az összegző függvény szimbólumát, a szigmát (∑) használjuk.
Amikor az összegző függvényeket határokkal együtt használjuk, a jelölés így néz ki:
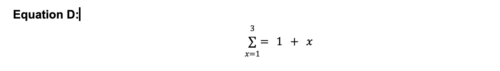
D) egyenlet
Vagyis elvégezzük a 1 + x számítást, minden alkalommal behelyettesítjük és növeljük az x értékét 1-től kezdve egészen 3-ig, és a végén összeadjuk az összes eredményt. Végül egy szép, rendezett egyenletet kapunk, ami kifejezi azt, ami kezdetben 3 különálló egyenlet volt, és ezekhez jön egy negyedik egyenlet, ami mindhárom eredményét összeadja.
Hát nem gyönyörű? Kezdetben kicsit ijesztő és elrettentő volt, de végülis csak egy sor egyszerű összeadásról van szó.
Most, hogy megértettük a Bitcoin kínálati képletében használt szimbólumokat és matematikai jelöléseket, nézzük meg az egyenlet egyes számait, és vegyük át, hogy mit jelentenek. Ígérjük, hogy a végén minden összeáll, még ha most kicsit nehéz is elképzelni.
i=0 – Ez az egyenlet alsó határa, ami az idő kezdeti epocháját jelöli. Amikor a Bitcoin protokollt először felfedezték, az első epochában voltunk, ami i=0 volt. Minden felezési epochában az i érték +1-gyel növekszik.
32 – A 32 az egyenlet felső határa. A 32 jelzi a BTC protokollon belül bekövetkező összes felezési epocha teljes számát. A felezési időszakokban az i értéket 0-ról (az alsó határ) 32-ig (a felső határ) növelik.
210 000 – Az egyes felezések blokkjainak száma. Minden 210 000 blokkból álló időszakot egy epochának neveznek. Minden 210 000 blokkból álló epocha után az összegző függvény határa (i) +1-gyel növekszik. A Bitcoin protokoll kifejezetten úgy van tervezve, hogy az új blokkok kiadásának ütemét átlagosan 10 percenként egy blokkra szabályozza. Így körülbelül ~4 évbe (210 000 x 10 perc) telik, míg egy 210 000 blokkos epocha lezárul.
50 – A Bitcoin történetének első epochájában a kezdeti blokkjutalom 50 volt. Azonban, ahogy hamarosan látni fogjuk, ez a szám minden epochában feleződik.
2 – Ez a szám jelöli a „felezést”. Minden epocha végén a blokkjutalmat kettéosztják, más szóval… felezik.
„i” = Ahogy fentebb említettük, az összegző függvény során az i érték az összegző függvény határain belül növelik, hogy megfeleljen az aktuális epochának. Az első epochában az i értéke 0 volt. A második epochában az i értéke 1. Amikor az i-t behelyettesítjük az egyenletbe, az a 2-es szám kitevőjeként (hatványaként) működik.
Például: Amikor i = 3, az egyenletben most 2^3-at látunk, ami alapvetően azt jelenti, hogy 2 a 3. hatványon, vagyis 2 x 2 x 2. Hasonlóképpen, ha az i egyenlő lenne 4-gyel, az tulajdonképpen 2 a 4. hatványon (2^4). A kitevő tehát közvetlenül befolyásolja a felezés blokkjutalmát (ami kezdetben 50 volt) minden epochában, és gyakorlatilag a 2-es szám kitevője.
Most, hogy mindezt tisztáztuk, rakjuk össze az egészet.
Végezzük el a Bitcoin kínálati képletét
Az összegző függvény elvégzéséhez korábbi példáinkhoz hasonló módon fogunk eljárni. Végrehajtjuk az egyenlet minden részét az i=0-tól kezdve egészen a 32-ig, majd a végén az egészet összeadjuk. Vegyük elő ismét a képletünket:
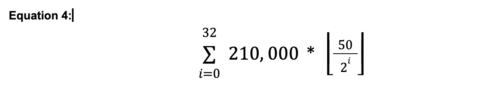
Az első körben behelyettesítjük az i=0-t az egyenletbe a Szigma (∑) jobb oldalán, elvégezzük az egyenletet, és rögzítjük a választ.
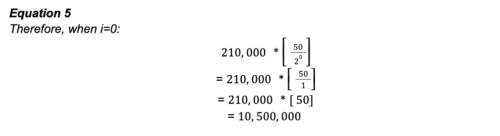
A számítás válasza megfelel a Bitcoin első epochájában (i=0) kibocsátott teljes bitcoinkínálatnak, amikor is 10 500 000 BTC került kibocsátásra jutalomként a bányászoknak. Az összegző függvény szabályait követve, amikor a bitcoin időlánc elérte a 210 000 blokkmagasságot, a protokoll növelte az „i” értékét, hogy megfeleljen a következő epochának (amikor i=1). Végezzük el újra az egyenletet, és adjuk hozzá az eredményt a meglévő nyilvántartásunkhoz.
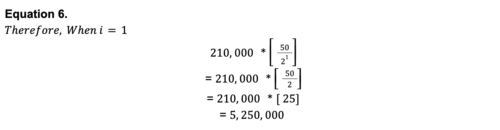
Ahogy fentebb is láthatjuk, a második epochában, ahol i=1, tekintettel arra, hogy a blokkjutalom az első epochában 50-ről (amikor i=0) a második epochában 25-re csökkent (amikor i=1), csak 5 250 000 bitcoin került bányászásra.
Most adjuk össze mindkét epocha kínálatát, hogy lássuk, mennyi bitcoin
 BTC Price
volt forgalomban a második epocha után.
BTC Price
volt forgalomban a második epocha után.
![]()
Ahogy a 3. epochába lépünk, egyszerűen növeljük az i-t +1-gyel, és újra elvégezzük az egyenletet. Ahogy haladunk, folyamatosan adjuk össze az egyes epochák számításainak összegét.

Mostanra már átlátjuk a mintát: ahogy epocháról epochára haladunk, az i értéket minden alkalommal +1-gyel növeljük, és kiszámítjuk az ellátás kibocsátását minden 210 000 blokkos epochára.
Így már kezd világossá válni, hogy a blokkjutalom hogyan feleződik minden egyes alkalommal, amikor az i értéket növeljük. Az első epochában 50-es blokkjutalomról indultunk, a másodikban 25-re, a harmadikban 12,5-re csökkent. És ez így fog folytatódni az utolsó epocháig, amikor i=32.
A blokkjutalmak minden epochában feleződnek. Ahogy tovább haladunk, az egyenletben szereplő „i” kitevő továbbra is kihat a blokkjutalomra, minden alkalommal felezve azt, amíg el nem érjük az összegző függvényünk felső határát, amikor is i=32.
Most végezzük el az egyenleteket egyenként, amíg el nem érjük az i=32-es felső határú végső epochát.
A bemutatáshoz Excelt használunk a munkánk maradék részének elvégzésére (3. ábra).
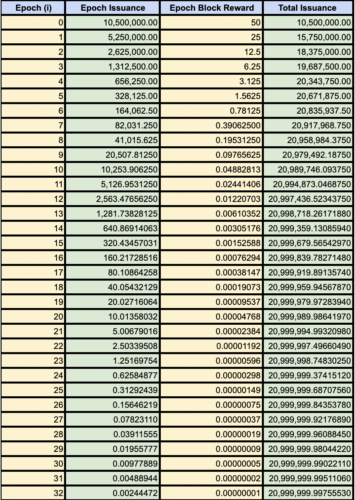
3. ábra: Az egyes epochák számítási eredményei
A 3. ábra számainak tanulmányozása során észrevehetünk valamit. Gyakran emlegetik, hogy a BTC érmék fix kínálati plafonja 21 000 000 bitcoin. Ha azonban időt szánunk a számítások elvégzésére, láthatjuk, hogy valójában soha nem érjük el pontosan ezt a számot. Körülbelül 244 470 satoshi-val maradunk el a 21 000 000-tól.
Remélhetőleg ezzel valamivel érthetőbbé vált, hogyan működik a Bitcoin kínálata, és talán megfakult matektudásunk is új életre kelt.